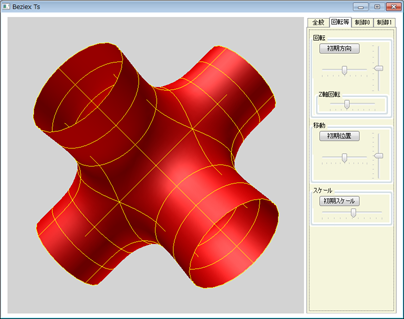
Beziex Ts (Home)
Beziex Ts (Home)
& ダウンロードへ
Beziex Pcc
Beziex Pcc C# (New!!)
リンクページへ
Eishin's Lab Roomへ
[メールフォーム]
Beziex LG (初代Beziex)
Beziex AT プレリリース版
(改良型Beziex)
-->[開発中止]
Copyright 1999-2016 EISHIN,
|
 Beziex自由曲面バーチャル研究室
Beziex自由曲面バーチャル研究室
(C)1999-2016 EISHIN, All Rights Reserved.
BeziexLab は、自称 CG理論アーキテクトの EISHIN が運営する私設バーチャル研究室です。この研究室は自由曲面理論の研究を目的としており、本サイトでは現時点までの成果である
のダウンロード (FREE) などを行っております。
なおこのページでは 「Beziex Ts」 について説明します。
■■■ Beziex Ts ■■■
1. 概要
Beziex Ts は「Beziex LG (初代 Beziex)」「Beziex AT」の曲面技術をさらに発展させた新アルゴリズムに基づく
である。
すなわちこれまでのように「自由曲面モデリング関数ライブラリ&サンプル」という構造では無く、新アルゴリズムにより生成された形状を視覚的に見るための
というニュアンスが強い。
なおツールといっても、ダウンロードファイルの中にはそのまま動作可能な実行ファイルは含まれていない。プロジェクトファイル&ソースファイルという形で入っているので、各自ビルドする必要がある。そしてこれも、すべてのソースコードを公開することにした。ちなみにこのソースコードは研究用なので、品質は保証しない。
また今までは開発言語として C++ を使用していたが、Beziex Ts では C# を使っている。つまりビルドの際はこの開発環境も用意しなければならない(ただし無料で揃えることが可能)。
2. Beziex Ts テクニカルガイド
本ページには Beziex Ts に特化された内容しか記述されていない。自由曲面に関する知識等は、下記のリンクにある「Beziex Ts テクニカルガイド」という PDF ファイルに収めてある。
そこで、「3. Beziex Ts 開発開始までの経緯」以降を閲覧する前に、この PDF を読まれることをお勧めする。
3. Beziex Ts 開発開始までの経緯
2004年当時、Beziex LG より進んだアルゴリズムを使用した Beziex AT をプレリリースしてみたものの、「やっぱり満足できるアルゴリズムでは無い」ということで開発を一時中断し、新アルゴリズムをひたすら考える日々が続いた(実際には研究を行なっていない時期の方がかなり多いが)。
2008年後半になって、まだ不満はあるが一度プログラミングしてみようというレベルのアルゴリズムが完成。プログラムを作成することにした。
当初 Beziex AT に新アルゴリズムを載せる予定であったが、元々 Beziex の研究を始めたのは「より良い曲面アルゴリズム」を見つけるためだったので、Beziex AT では良くないという結論に至ることとなった。
具体的にはまず
| |
各形状ごとにベストの要素値を与えた上で、出来上がった形状が綺麗であるかどうか判断しなければならない
|
ということがあげられる。Beziex AT は「どんな形状であってもある程度対応できる」計算値を要素に用いて形状を作成しているので、汎用的ではあるが「各形状ごとにベストの要素値」とはなっていない。
汎用的な要素値だと形状が綺麗で無かった場合、「要素値が悪い」のかあるいは「アルゴリズムが悪い」のか判断が付かないのである。これに対しベストの要素値で形状が綺麗で無い場合は、「アルゴリズムが悪い」ということだ。
ただし「各形状ごとにベストの要素値」とするためには、各形状の要素をそれぞれソースコードで記述し、各自適した計算を行なって求めなければならなくなる。つまり Beziex LG や Beziex AT で使用した
| |
「最小限の情報を記述したファイル」から形状を求める
|
ことは出来ず、拡張性が乏しくなるわけである。もちろんユーザー側で新たなソースコードで記述すれば別の形状を作ることも可能であるが、結構難しい。
しかし本来の研究目的を考え、汎用性は捨てることにした。つまりデータファイル等は使用せず、基本的に特定の形状のみが生成されるようにしたのである。
なお現状の Beziex Ts でも形状によっては「ベストの要素値」がどれぐらいなのか確定できないものもあった。これについては今後の課題であるが、とりあえず現時点で設定した計算値であっても「汎用の計算値」よりはベターであると思われる。
次に今後アルゴリズムの改良を行なった際、
ということがあげられる。つまりプログラム自体に表示機能が無くてはならない。これはコマンドラインプログラム(すなわち Beziex AT)では無理である。
また形状は3Dなので「形状の3D回転機能」が必要で、また細部を目視するためには「形状の移動&スケーリング機能」も無くてはならない。Beziex LG には表示機能および回転等の機能は付いていたが、回転角などを数値で与えなければならず、とても使いにくいものであった。
これらを使いやすくするためには何らかのGUIが必要となるが、Beziex LG の開発当時は簡単にコーディング出来るものが無かったのである。なお頑張れば作れたと思われるが、(曲面アルゴリズムの研究が主目的なので)GUIにあまり時間を割きたくないのも事実である。
ところで最近は Beziex LG 開発当時に比べ、3D表示用ライブラリやGUI開発環境も増えてきた。特にGUIに関しては C# という開発言語を使うと簡単そうである。
なお C# は C++ と比べて計算速度が遅いので、「曲面生成処理は C++」「表示やGUIは C#」とすることも考えたのだが、それでは手間が増える。そこですべて C# でコーディングすることに決めた。今のPCは速いので、それでも問題無いであろう。
4. 新アルゴリズム
Beziex の曲面アルゴリズム研究は「隣接曲面との滑らかさ」の向上を第一目的としている。そこで「隣接曲面との滑らかさ」について、少し詳しく述べることにする。
まず Bezier 系曲面の内部制御点の位置は
| a) |
境界曲線 |
| b) |
「境界横断導関数(CBD=Cross Boundary Derivative)」(微分値の一種) |
によって決まる。そしてこの CBD が特定の条件の場合に隣接曲面どうしが滑らかに繋がるわけである(すべての Beziex はこの条件を満たしている)。さらに
| c) |
「a) 上で任意値の媒介変数(t) の点を原点として、同値の t の b) を延ばした先端」を全ての t値で結んだ曲線 |
を考えた場合、通常この c) 曲線が綺麗な形をしているときに滑らかさが向上することが多い。
しかしこれまでの Beziex では、最初に各要素値を与えると自動的に c) が決まってしまい、しかもその c) 曲線が綺麗なのかどうかは予測できなかった。
そこで、
| |
最初に「理想 c) 曲線」を設定し、実際の c) 曲線をなるべく「理想 c) 曲線」に近くできるようなアルゴリズム
|
を考案し、Beziex Ts に採用した。
もちろん「隣接曲面との滑らかさ」はこれだけで決まるわけでは無く、曲率や平滑性なども影響する。例えば隣接曲面どうしで曲率が大きく異なる場合、実際には滑らかにつながっている(折れ曲がってはいない)にも関わらず、人間の目には折れ曲がっているように見えることもあるのである。
このように改良すべき点はたくさん残されているが、これらについては Beziex Ts のアルゴリズム等をベースにして徐々に解決していきたいと思っている。
5. 特長(抜粋)
5-1. 延長境界曲線
Beziex Ts v0.9.3 では「延長境界曲線」をサポートした。「延長境界曲線」とは、「1個の曲面の一辺」である境界曲線よりも長い曲線のことで、v0.9.3 では「2面延長境界曲線」のみに対応している。
"隣合う2曲面の共有境界曲線" の一方の頂点を共有するこれらの面の境界曲線(側辺)は2本(各面に1本ずつ)ということになるが、この "2本の境界曲線" が1本の3次ベジェ曲線で表せる時、("各面ごとに境界曲線を設定" するのでは無く)まとめて1本の状態で設定出来るようにした。これを「2面延長境界曲線」と呼ぶことにする。
なお v0.9.3 では「2面延長境界曲線」内の中間頂点の位置は、パラメータ的には必ず t=0.5 の位置とする。また Beziex Ts は研究用プログラムなので、とりあえず4角曲面でのみ「延長境界曲線」に対応した。ちなみに「2面延長境界曲線」をさらに拡張して、3面以上の「延長境界曲線」も可能なはずだが、研究用ということで2面に限定することにする。
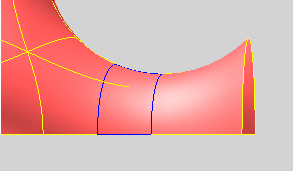
ところで下図は「全般」タブのオブジェクト「ExtendEdge0」の一部であるが、青い曲線が「延長境界曲線」である(2本存在する)。実際に Beziex Ts を実行して確かめる場合は、「全般」タブの
| ・ |
「オブジェクト」を "ExtendEdge0" |
| ・ |
「境界曲線を表示(全体モード時)」をON |
| ・ |
「境界曲線の別色化」の「標準情報 + 延長境界」をON |
とすること。
なお制限として、1個の面(4角曲面)に使える「延長境界曲線」は2本までで、且つ「延長境界曲線」の端の頂点は必ず最初から設定された状態でなければならない。
また「延長境界曲線」を挟んで両側に面を設定する(隣接面となる)ことが出来るが、Beziex Ts v0.9.4 からは、例えば
とすることが可能となった。
例として "SixRadial2" を挙げた場合、これは "SixRadial1" の各末端(断面が円になっている)に円錐台が付いている形となっている。しかし "SixRadial1" の末端の円は8個の円弧から成り、円錐台の断面は4個の円弧から成る。
通常これを繋ぐことは出来ないが、「延長境界曲線」を使うことでそれが可能になった。ただしこのままでは、この両者を滑らかに繋ぐことは出来ない。
5-2. オーバーレイ
上記で「"延長境界曲線" の左側に2個の面、右側に1個の面」に対応したことを記述したが、両者は滑らかに繋がっていない。そこでこの場合でも滑らかに繋がるようにするため、Beziex Ts v0.9.5 では「オーバーレイ」という機能を追加した。
上図は「全般」タブのオブジェクト「SixRadial3」の一部であるが、この図を例に取ると、青枠(4本の青い境界曲線から成る4角曲面)で囲まれた領域がオーバーレイである。このうち左右の青い境界曲線は「延長境界曲線」になっており、上下の青い境界曲線は通常の境界曲線("非"延長境界曲線)である。このような構造になっている時にのみ、オーバーレイを使うことが出来る。
オーバーレイとはこの図の場合、
| ・ |
青枠にはまり込むように、上下に隣接する2個のベース曲面がある。この2曲面の間の境界曲線(オーバーレイ中央境界曲線)は、青枠内に途中(曲面の中央辺り)まで描画されている黄色の境界曲線であるが、実際には右端まで延びている(表現上、わかりやすくするため途中までしか描画していない)。また他の境界曲線は青枠上にある。 |
| ・ |
2個のベース曲面の上に、青枠と同じ境界曲線を持つ1個のオーバーレイ曲面が乗っている。 |
| ・ |
実際にはベース曲面とオーバーレイ曲面は混合された状態となっている。そして左側の境界曲線上では(2個存在する)ベース曲面の CBD が隣接面と滑らかに繋がっており、右側の境界曲線上では(1個しかない)オーバーレイ曲面の CBD が隣接面と滑らかに繋がっている。
また上下の青い境界曲線上の CBD は、ベース曲面とオーバーレイ曲面で幾何学的に同一となっている。 |
これによりオーバーレイを介して、左側は2個の面で且つ右側は1個の面とし、さらにそれらを滑らかに繋げることが出来たわけである。
5-3. パッチ型 Catmull-Clark サブディビジョン
Beziex Ts v0.9.9 では「パッチ型 Catmull-Clark サブディビジョン (Patch-type Catmull-Clark subdivision : PCC)」をサポートした。
この「パッチ型 Catmull-Clark サブディビジョン」は、"Catmull-Clark サブディビジョン" によって生成された曲面 (実際にはポリゴンの集まり) を、パラメトリック曲面 (パッチ) に近似変換したものである。Charles Loop、Scott Schaefer による「近似 Catmull-Clark サブディビジョン (Approximating Catmull-Clark subdivision : ACC)」と良く似ているが、変換アルゴリズムは異なっている。
なお変換後のパッチは Beziex 曲面となるので、これを「Beziex PCC」と呼ぶことにする。この「Beziex PCC」の最も基本となる形状は、下図の通りとなっている。ちなみに図内の青線は、サブディビジョンの元となったポリゴンの輪郭である。
6. 実験的データ
6-1. 境界横断導関数を曲率 0 にして接続
まず「a) "SixRadial3" 先端のラッパ状の筒を取り除いた形状」や「b) FourRadial5」の先端境界曲線の境界横断導関数(CBD)は「非 0 の曲率」である。そして仮にこれらの先端境界曲線にぴったり合う円筒を接続した場合、この円筒の共有境界曲線のCBDの曲率は 0 である。
ちなみに a) や b) と円筒は滑らかに接続されている。しかしCBDの曲率は大きく異なることになる。このような場合、(滑らかに接続されているにも関わらず) ハイライト(スペキュラー)が折れ曲がったりするので、滑らかに接続されていないように見えることがある。
これを解消するためには a) や b) の共有境界曲線のCBDの曲率の方も 0 にすれば良い。また a) や b) と円筒のCBDの向きも一直線になるようにする。
そこで Beziex Ts v0.9.7 では、CBDがそのようになっているデータである「SixRadial4」や「FourRadial8」を作成してみた。境界曲線を表示してみると、先端に円筒が付加されていることが分かるが、中心部分とこの円筒は見た目上も滑らかに接続されていることが確認出来る。
なお実は a) や b) で完全に曲率が 0 なのは、共有境界曲線の頂点部分のCBDだけで、曲線の内部は 0 では無い。ただし 0 にかなり近いので、実験的な意味合いでは問題無いだろう。
ちなみに3次ベジェ曲線の境界曲線で曲率を 0 にするのは、かなりの制約がある。ただ4次以上(6次以上を推奨)にしても、曲率をコントロールしようとすると境界曲線形状に制約が出てきてしまうので、「曲率と形状を両立させることは難しい」ことには変わりは無い。
よってこれに関しては、どこで妥協するかの問題になってくるものと思われる。
7. 開発/実行環境
7-1. OS/解像度
7-1-1. 稼動OS
Beziex Ts をビルド&実行できるOSは Windows のみである。Windows のバージョンは「6-3. 開発/実行環境のダウンロード」の環境が動くものであれば大丈夫だと思うが、現在のところ Windows 7 SP1 (v0.8.9a までは Windows XP SP3、v0.9.0b までは Windows 7 SP無し) 上でしか試していないのでご容赦願いたい。
7-1-2. 解像度
解像度は「1024 × 768」以上でなければならない(縦横ともこの解像度を下回らないこと)。また色数は「True Color (32 or 24ビット)」以上が望ましい。
7-2. 使用技術
Beziex Ts では以下のような開発/実行環境を使用している。
1) C# コンパイラ
| |
「Microsoft Visual C# 2010 SP1」を使用 (v0.8.9c までは「Microsoft Visual C# 2008 SP1」、2010版の「SP無し」→「SP1」への移行バージョンは不明) 。
|
2) .NET Framework
| |
「.NET Framework」は C# と密接な関係にある。「Microsoft Visual C# 2010」をインストールすると「.NET Framework 4.0」もインストールされるようだが、場合によっては別途インストールしたり、.NET Framework 2.0, 3.0, 3.5 もインストールする必要があるかもしれない。
|
3) WPF(Windows Presentation Foundation)
| |
ユーザーインターフェイス開発/実行用環境であり、これがあるので開発言語を C# にしたといっても過言では無い。
なお Visual C# にはユーザーインターフェイス開発環境として「Windowsフォーム」と「WPF」の2種類があるが、WPF の方が新しい技術であり、また構造が自分好みなので WPF を採用した。
ちなみに WPF を使用するためには「.NET Framework 3.0」以上が必須である。
|
4) DirectX(Direct3D)
| |
PC で 3D を表示させる際には、OpenGL もしくは DirectX の技術を用いることが多い。開発環境として C# を採用し、その上で 3D表示を行う場合は通常、「WPF の3D機能」「C# 用 DirectX」「XNA」「C# 用 OpenGL」のいずれかを使用する。このうち「WPF の3D機能」「C# 用 DirectX」「XNA」は DirectX系 、「C# 用 OpenGL」は OpenGL系である。
ちなみに当初「C# 用 OpenGL」のことは知らなかったので、必然的に DirectX系を使うことになった。また Windows XP 上でも稼動させたかったので、バージョン 9.0 をベースとした。
余談であるが現在「C# 用 OpenGL」では、「OpenTK」というのがちょっと有名らしい。ここは今でもまともに更新を続けているのだが、他の「C# 用 OpenGL」プロジェクトは活動しているのかどうかも不明といった感じである。
なお話を戻して、一番最初は「WPF の3D機能」を使用するつもりでいたのだが、機能が少なすぎて断念。また開発当時「Visual C# 2008 + WPF」の組み合わせでは「XNA」がうまく動かず、これも断念した。ちなみに XNA は Xbox 360 等にも使用されている技術である。残る選択肢は「C# 用 DirectX」ということになるが、これには Microsoft が提供する「Managed DirectX」やサードパーティ製などがある。
ただ当時はサードパーティのものを知らず、またその頃は(サードパーティ製は)とてもマイナーな存在だったらしいので、「Managed DirectX」を採用することにした。しかし Beziex Ts の製作開始時には、既に Managed DirectX の新たなバージョンは開発中止になっており、今後も更新されることは無さそうだ。ということで Managed DirectX を採用してみたものの、いつまでもレガシーな環境を使うのは良くないだろうと、常々思っていた(結局、v0.8.9e までは Managed DirectX を使うことになってしまったが)。
|
5) SlimDX
| |
サードパーティ製「C# 用 DirectX」は(Beziex Ts の)開発当初マイナーな存在だったが、その後サードパーティ製の一つである「SlimDX」が多少有名になってきた。フリーであるが今後の更新も期待でき、また DirectX 機能の多くを網羅しているので、Managed DirectX の後継と考えて問題無いだろう。
ということで、v0.9.0 からは「SlimDX」を使用することにした。
ちなみに「XNA」は、使用 C# コンパイラのバージョンが限定されていたりして、開発の自由度に欠けるので、今のところ使う予定は無い。
なお2012年になって、「SharpDX」というサードパーティ製ライブラリも少し有名になってきた。ただ SharpDX は頻繁にバージョンアップし過ぎる(1〜2ヶ月単位)。それに対し、SlimDX は1年に2回ぐらいだ。
Beziex Ts は各自、必要なツール&ライブラリをダウンロードし、自分でビルドするスタイルを取っているので、なるべく最新のツール&ライブラリに対応させたい。しかしバージョンアップが頻繁だと、それも大変なのである。ただ SharpDX も SlimDX 同様、過去のバージョンをダウンロード可能なので、対応が間に合わない時は、古いバージョンを取得してもらえば問題無いのだが。
ちなみに SlimDX→SharpDX の移行は簡単らしく、また SharpDX は SlimDX よりも最新の環境に対応しているようなので、必要性が出てくれば移行することにする。
|
7-3. 開発/実行環境のダウンロード
7-3-1. Microsoft Visual C# 2010 SP1
| |
Microsoft Visual C++ 2010 Express Edition - 日本語用
|
| |
を用いてビルドを行なった。このツールは無料でダウンロード可能である。具体的には下記のような操作でインストールすればよい。
|
| |
1) |
開発環境が Windows 7 で且つ、まったく「ISO仮想ドライブソフト」が入っていない時は、何らかの仮想ドライブソフトをインストールしなければならない。
例えば「WinCDEmu」というソフトを使う場合は、下記URLの「Download」ボタンを押し、インストーラをダウンロードする。そしてインストールを行うこと。
|
| |
2) |
下記URL(直リンク)から "Visual Studio 2010 Express" の「オフライン(DVD)インストール版」をダウンロード。
|
| |
3) |
「VS2010ExpressJPN.iso」をダブルクリックして、マウントする。
|
| |
4) |
「setup.hta の実行」を行う。そして途中、「Visual C++ 2010 Express」を選択。
|
| |
5) |
「VS2010ExpressJPN.iso」のインストールを最後まで実行したら、下記URLで Service Pack 1 をダウンロードし、インストールする。
|
| |
なお当コンパイラをインストールすると、「.NET Framework 4.0」もインストールされ、また WPF も使用できるようだ。
ちなみに .NET Framework 2.0 や 3.0 もインストールする必要が出てきた場合は Windows Update (Microsoft Update) で「カスタム」を選べばインストール可能である。
なお Beziex Ts は、Visual C# 2010 だけを用意してもビルドできない。以下の2種類のライブラリを追加ダウンロードする必要がある(有料版 Visual Studio 2010 には、DirectX SDK の方は入っている可能性があるが)。
|
7-3-2. June 2010 DirectX SDK
| |
からダウンロードすればよい(英文)。「DXSDK_Jun10.exe」というファイルが
|
| |
から取得出来るので、ここからダウンロードする。
なお「DirectX SDK」をダウンロードする際は、下記の「SlimDX SDK」に対応しているものをダウンロードすること。ちなみに「June 2010 DirectX SDK」には、
|
| |
SlimDX SDK (January 2012).msi |
| |
SlimDX SDK (September 2011).msi |
| |
SlimDX SDK (March 2011).exe |
| |
SlimDX SDK (June 2010).exe |
| |
が対応している。
すなわち「DirectX SDK」のバージョンの中で、SlimDX SDK に対応しているものを選ばなければならない。
|
7-3-3. SlimDX SDK (January 2012)
| |
からダウンロードすればよい。「Featured」→「Downloads」の項に
|
| |
「SlimDX SDK (???? ????).msi」のリンク
|
| |
が存在するので、ここからダウンロードする。ちなみに「(???? ????)」の部分には、DirectX SDK と同じく "リリース年 & 月" が記述されており、(January 2012) のようになっている。
なお過去の「SlimDX SDK」は
|
| |
からダウンロードする。ここに「Beziex Ts で使用している日付の SlimDX SDK」のリンクがあるはずなので、それをクリックする。そして "Developer SDK" の項に
|
| |
「Install Developer SDK」ボタン
|
| |
があるので、それを押してダウンロードすればよい。
ちなみに Beziex Ts では、「SlimDX SDK (January 2012).msi」を用いてビルドした。
なお昔の「SlimDX SDK」は、「DirectX SDK」の "リリース年 & 月" の部分と同じものを使用することになっていた。つまり SlimDX の方が公開スケジュールを同期させているわけである。しかし DirectX SDK は June 2010 以降まったくリリースされないので、もう待てないということで SlimDX 側が非同期のリリースに踏み切ったようだ。
|
7-4. ビルド時の注意事項
開発/実行環境のインストールが終わったら、「BeziexTs.sln」を起動しビルドを行なう。この際、DirectX SDK や SlimDX SDK のインストール先やバージョンによっては、
| |
Visual C# から SlimDX がうまく見つけられない
|
場合も有り得る。その時はソリューションエクスプローラの「参照設定」を修正し、以下のクラス
が参照できるようにしなければならない。なお参照設定の各クラスにはバージョンが存在するが、SlimDX のバージョンはおそらく1種類だけだと思われる (複数の「SlimDX SDK」をインストールしていない限りは)。
ちなみに SlimDX を追加するときは,
| 1) |
「参照設定」内に適切でない SlimDX がある場合は、その SlimDX を右クリックメニューで「削除」する。 |
| 2) |
「参照設定」の右クリックメニューから「参照の追加」→「参照」タブで |
| |
C:\Program Files\SlimDX SDK (???? ????)\Bin\net40\x86\SlimDX.dll
|
| |
を選択する(デフォルトインストール時)。ただし「SlimDX SDK (June 2010)」より前のバージョンの場合は定かでは無い。 |
とする。「(???? ????)」の部分は、同じく "リリース年 & 月" である。なお「...\Bin\」より後ろの部分には、"(June 2010)"〜"(January 2012)" の場合、
| | net20\x86 |
| | net20\x64 |
| | net40\x86 |
| | net40\x64 |
の4種類の SlimDX.dll が存在する(Beziex Ts では "net40\x86" を使用)。このうち "x64" は 64bit版Windows 専用であるが、私 (EISHIN) は試したことは無い。
ちなみに "net40" は「.NET Framework 4.0」用である。「.NET Framework 2.0〜3.5」用の SlimDX.dll である "net20" を使用する場合は、「ソリューションエクスプローラ」→「BeziexTs」の右クリックメニューで「プロパティ」→「アプリケーション」タブを選択し、「対象のフレームワーク」を ".NET Framework 3.5" にする(一応、このようにしても動くようである)。
8. BeziexTs.exe の使い方
Beziex Ts を動かすためには、「BeziexTs.sln を読み込んだ Visual C# 2010 (もちろんビルド済みのもの)」上から走らせるか、「BeziexTs.exe」を起動する。
そして起動後の使用方法は、以下の通りである。
8-1. 「全般」タブ
8-1-1. 「オブジェクト」
表示したい形状を選択する。
8-1-2. 「面の色を濃い目にする」
これをONにすると、濃い目の面の色となる (v0.8.9a までは濃い目がデフォルト)。
8-1-3. 「面をメッシュ状にする」
これをONにすると、面がメッシュ状(網状)になる。
8-1-4. 「境界曲線を表示(全体モード時)」
これをONにすると、境界曲線を表示する。全体モード時のみ有効。
8-1-5. 「ベースポリゴンを表示(CCSubdivデータの場合)」
これをONにすると、"Catmull-Clark サブディビジョン" の元となったポリゴンの輪郭を表示する。CCSubdivデータ(「Beziex PCC」のデータ)の場合のみ有効。
8-1-5. 「表示種別」
1) 「全体モード」
| |
このラジオボタンをONにすると、形状全体を表示する。
|
2) 「面モード(選択前)」 & 「面モード」
| |
「面モード(選択前)」ラジオボタンをONすると、「境界曲線を表示(全体モード時)」チェックボックスのON/OFFに関わらず、境界曲線が表示される。ここで "形状のどれかの面(境界曲線で囲まれた内部)" をクリックすると、ラジオボタンが「面モード」に変わり、その面だけが表示されるようになる。
また「面モード」時に "面のどれかの境界" をクリックすると、その境界曲線が表示/非表示される。具体的には、境界曲線が非表示の時にクリックすると表示され、表示されている時にクリックすると非表示となる。境界曲線が表示されている時は、さらに「制御0」タブの「面モード(境界曲線単位)」内でONとなっている情報も表示する。
なお Beziex Ts では、"内部制御点の元となる「基準内部制御点」" を下記のように2種類の方法で定義出来る。
|
| a. |
基準となる「等パラメータ線(1/3値)」 (「等パラメータ線(1/3値)」項目の "初期値" の元となる値)。 |
| b. |
基準となる「境界横断導関数(CBD)」(後述)。パラメータ値が1/3と2/3のCBDを指定する。ただし現在のところ、4角曲面にのみ対応。 |
| |
その際、境界をクリックした際に表示される境界曲線の色は、a.の場合は黄、b.の場合は緑となる。
|
3) 「隣接面モード(選択前)」 & 「隣接面モード」
| |
「隣接面モード(選択前)」ラジオボタンをONすると、「境界曲線を表示(全体モード時)」チェックボックスのON/OFFに関わらず、境界曲線が表示される。ここで "形状のどれかの境界曲線" をクリックすると、ラジオボタンが「隣接面モード」に変わり、"その境界曲線に隣接する面(2個 or 1個)" だけが表示されるようになる。
"オーバーレイ中央境界曲線" をクリックした場合は、(隣接する)2個のベース曲面を表示する(混合されるオーバーレイ曲面は非表示)。
|
4) 「周回面モード(選択前)」 & 「周回面モード」
| |
「周回面モード(選択前)」ラジオボタンをONすると、「境界曲線を表示(全体モード時)」チェックボックスのON/OFFに関わらず、境界曲線が表示される。ここで "形状のどれかの頂点(境界曲線の交差する点)" をクリックすると、ラジオボタンが「周回面モード」に変わり、"その頂点の周りの面" だけが表示されるようになる。
|
5) 「再選択」ボタン
| |
「面モード」、「隣接面モード」、「周回面モード」のいずれかのとき(「選択前」では無い)、有効となるボタンである。このボタンをクリックすると、
|
| | 「面モード」 → 「面モード(選択前)」 |
| | 「隣接面モード」 → 「隣接面モード(選択前)」 |
| | 「周回面モード」 → 「周回面モード(選択前)」 |
| |
になる。これにより形状全体が表示される状態に戻り、面、境界曲線、頂点のいずれかが選択できるようになる。
|
8-1-6. 「投影方法」
1) 「透視投影」
| |
このラジオボタンをONにすると、透視投影で表示する。
|
2) 「平行投影」
| |
このラジオボタンをONにすると、平行投影で表示する。
|
8-1-7. 「境界曲線の別色化」
境界曲線の種類に応じて、該当する境界曲線を別の色(青)にする(通常は黄色)。
ちなみにこの境界曲線は、「全般」タブの「全体モード」と「境界曲線を表示(全体モード時)」がONの場合、もしくは「面モード」「隣接面モード」「周回面モード」のいずれかの時で "(選択前)" の状態になっている場合に表示する。
1) 「オーバーレイ境界」
2) 「各種境界情報」
| |
各種境界情報を別色(青)にする。
まず「標準情報/直接情報」の違いは、「標準情報」は近似円弧/楕円弧に必要な情報なのに対し、「直接情報」はベジェ曲線の制御点そのものの情報であることである(Beziex Ts v0.9.3 までは「標準情報」のみをサポートしていた)。
「延長境界/非延長境界」は「延長境界曲線」であるか否かであり、「延長境界曲線」については前述の通り。
|
| |
これをONにすると、「標準情報 + 非延長境界」の境界曲線が別色(青)になる。
|
| |
これをONにすると、「標準情報 + 延長境界」の境界曲線が別色(青)になる。
「全般」タブのオブジェクトの「ExtendEdge0」「SixRadial1」を参照のこと。
|
| |
これをONにすると、「直接情報 + 非延長境界」の境界曲線が別色(青)になる。
「全般」タブのオブジェクトの「EdgeDirect」「SixRadial1」を参照のこと。
|
| |
これをONにすると、「直接情報 + 延長境界」の境界曲線が別色(青)になる。
「全般」タブのオブジェクトの「SixRadial1」を参照のこと。
|
8-2. 「回転等」タブ
8-2-1. 「回転」
1) 「横スライダ」
| |
Y軸(縦軸)まわりに回転させる。動かすと「縦スライダ」、「Z軸回転」スライダは中心位置に戻る。
|
2) 「縦スライダ」
| |
X軸(横軸)まわりに回転させる。動かすと「横スライダ」、「Z軸回転」スライダは中心位置に戻る。
|
3) 「Z軸回転」スライダ
| |
Z軸(中心軸)まわりに回転させる。動かすと「縦スライダ」、「横スライダ」は中心位置に戻る。
|
4) 「初期方向」ボタン
8-2-2. 「移動」
1) 「横スライダ」
2) 「縦スライダ」
3) 「初期位置」ボタン
8-2-3. 「スケール」
1) 「スライダ」
2) 「初期スケール」ボタン
8-3. 「制御0」タブ
「面モード(境界曲線単位)」は、「全般」タブ→「表示種別」が「面モード」の時のみ有効 (「面モード(選択前)」時は無効)。
8-3-1. 「面モード(境界曲線単位)」
(「面モード」時に境界をクリックすることで表示される)境界曲線に対して、各情報を表示する。
1) 「境界曲線の制御線」
2) 「線数」
| |
境界曲線上に表示する「境界を横断する制御線」の本数を「11本」と「5本」から選択する。
|
3) 「境界を横断する制御線」
| |
「境界横断導関数(CBD)」のことである。「Beziex Ts」の CBD は、「境界曲線微分値をm倍したベクトル」(境界曲線接線)と「ベース境界横断導関数をn倍したベクトル」(ベースCBD)に分かれている(両者の内積が0に近くなるのがベスト)。また隣接面が共有する境界曲線上の(各面の)「ベースCBD」は、2面を通して一直線となる(隣接面が滑らかに繋がっている場合)。この「境界曲線接線」と「ベースCBD」を合成したものが「最終的な CBD」(補正境界横断導関数)である。
|
| | 非表示: | 「CBD 関連要素」を表示しない。 |
| | ベースCBD: | 「ベース境界横断導関数をn倍したベクトル」を表示する。 |
| | 最終形: | 最終的な CBD (補正境界横断導関数)を表示する。 |
| | すべて: | 境界曲線接線、ベースCBD、最終形の3種類の「CBD 関連要素」を表示する。境界曲線接線は厳密には、「境界曲線微分値をm倍したベクトル」である。 |
4) 「対面(3角曲面で有効)」 (「境界を横断する制御線」内)
| |
3角曲面の時に、"クリックした境界曲線" の反対側の頂点上の「境界横断導関数(CBD)」を表示する。
|
5) 「中間形(前-内部生成)」 (「境界を横断する制御線」内)
| |
「中間形(前-内部生成)」の段階(後述)での「境界横断導関数(CBD)」を表示する。
|
6) 「等パラメータ線(1/3値)」
| |
通常、パラメトリック曲面は2個のパラメータ値(u, v)で表されるが、ここでは u または v の値が 1/3 の時の曲線を表示する。
なお「制御1」タブ内 「オーバーレイ」の項目が「混合曲面」の場合、「最終形」以外は無効 (「最終形」と「3角曲面の情報」を除き、グレイ表示となる)。
|
| |
ソースコードに記述した要素値から最初に求まる 1/3 パラメータ値の曲線で、3次となる。これはまだ曲面化する前の "内部制御点の元となる曲線" である。
なお下記の場合は全非表示、または制限付きの表示となる。
|
| | - | (境界をクリックすることで表示される)境界曲線の色が緑の場合は、全境界で非表示。 |
| | - | 「制御1」タブ内 「オーバーレイ」の項目が「オーバーレイ曲面」の時で、(境界をクリックすることで表示される)境界曲線の色が黄色の場合、「延長境界曲線」についてのみ表示する。 |
| | - | 「制御1」タブ内 「オーバーレイ」の項目が「混合曲面」の場合、全境界で非表示。 |
| |
「初期値」を元にまず仮となる3次の内部制御点が作成されるが、その内部制御点から導き出された 1/3 パラメータ値の曲線。以前は「法線補正」と呼んでいたが、この補正を止めたので改称した。
|
| |
CBD を s成分, t成分に分離する処理を行った後の曲線で、高次の有理曲線となる。なお CBD の t成分が隣接面と一直線上にある場合に滑らかに繋がるが、これは「一直線となるように補正」する前の段階。
|
| |
「中間形(CBD補正前)」に t成分が「一直線となるように補正」を行ったもの。
|
| |
Beziex では「複数の Bezier 曲面を混合」して最終的な曲面としている。「中間形(CBD補正後)」までは 1個の Bezier 曲面上の曲線であったが、「最終形」では混合後の曲面から導いた曲線となる。
|
7) 「3角曲面の情報」
| |
3角曲面の時の「等パラメータ線」を表示内容を指定する。
|
| |
"クリックした境界曲線" に近い側の「等パラメータ線」(v値が1/3)を表示。
|
| |
"クリックした境界曲線" から遠い方の「等パラメータ線」(v値が2/3)を表示。
|
| |
"クリックした境界曲線" の方向である u方向 では無く、v方向の「等パラメータ線」を表示(u値は1/2)。
ただし「初期値」の時は "縦(1/2値)" 曲線を求め得る前の状態なので、表示しない。また「中間形(CBD補正前)」「中間形(CBD補正後)」「最終形」の時は、頂点が特異点になるので、頂点付近は表示しない。
|
| |
クリックした境界曲線から延びる "縦(1/2値)" の「等パラメータ線」は、他の2本の "縦(1/2値)" の「等パラメータ線」と交差する ("中間形(法線補正)" の「等パラメータ線」)。
その交差する点2個の平均値を表示。なお交点は点の形では無く、法線方向に延びる直線として表示される。
|
8-4. 「制御1」タブ
8-4-1. 「面モード(全体)」
「面モード(全体)」は、「全般」タブ→「表示種別」が「面モード」の時のみ有効 (「面モード(選択前)」時は無効)。
1) 「オーバーレイ」
| |
「面モード」でオーバーレイ箇所を選択した場合に表示する曲面を指定する。
|
| |
「オーバーレイ曲面」を表示する。「面モード」で(境界をクリックすることで表示される)境界曲線の色が黄色の場合、「制御0」タブ内 「等パラメータ線(1/3値)」の「初期値」は「延長境界曲線」についてのみ表示する (境界曲線の色が緑の場合、「等パラメータ線(1/3値)」の「初期値」は元々表示しない)。
|
| |
「ベース曲面」と「オーバーレイ曲面」を混合した曲面を表示する。「制御0」タブ内 「等パラメータ線(1/3値)」の項目は、「最終形」のみが有効である (「等パラメータ線(1/3値)」の項目は「最終形」と「3角曲面の情報」を除き、グレイ表示となる)。
|
2) 「法線」
| |
これをONにすると、面上を等パラメータ間隔で法線を表示する。
|
8-4-2. 「隣接面モード」
以下は、「全般」タブ→「表示種別」が「隣接面モード」の時のみ有効 (「隣接面モード(選択前)」時は無効)。
1) 「境界曲線」
| |
これをONにすると、境界曲線を表示する(隣接面がある境界曲線のみ)。
|
2) 「境界曲線の制御線」
3) 「線数」
| |
境界曲線上に表示する「境界から延びる法線」、「境界を横断する制御線」の本数を「11本」と「5本」から選択する。
|
4) 「境界から延びる法線」
| |
これをONにすると、境界から延びる法線を表示する。
|
5) 「境界を横断する制御線」
| | 非表示: | 「CBD 関連要素」を表示しない。 |
| | ベースCBD: | 「ベース境界横断導関数をn倍したベクトル」を表示する。 |
| | 最終形: | 最終的な CBD (補正境界横断導関数)を表示する。 |
| | すべて: | 境界曲線接線、ベースCBD、最終形の3種類の「CBD 関連要素」を表示する。境界曲線接線は厳密には、「境界曲線微分値をm倍したベクトル」である。 |
8-4-3. 「周回面モード」
以下は、「全般」タブ→「表示種別」が「周回面モード」の時のみ有効 (「周回面モード(選択前)」時は無効)。
1) 「境界曲線」
| |
これをONにすると、境界曲線を表示する(隣接面がある境界曲線のみ)。
|
2) 「頂点から延びる制御線」
| |
これをONにすると、境界から延びる制御線(微分値)を表示する。
|
3) 「頂点から延びる法線」
| |
これをONにすると、境界から延びる法線を表示する。
|
9. 履歴
9-1. 履歴(プログラム)
2009/05/17
2009/06/06
| | v0.8.5 |
「"(補正)境界横断導関数"用パラメータを生成するためのマトリックス」 M について、この M を決定するためのアルゴリズムを改良。 |
2009/09/23
2009/10/09
| | v0.8.9 |
「全般」タブの「表示種別」に「周回面モード」を追加。 |
2009/10/18
| | v0.8.9a |
「全般」タブに「面をメッシュ状にする」を追加。 |
2009/12/31
| | v0.8.9b |
「制御線」タブを追加(「隣接面モード」と「周回面モード」)し、また「全般」タブに「面の色を濃い目にする」を追加。
さらに Windows 7 で (おそらく Windows Vista でも) 表示文字が欠ける不具合を修正した。なお私 (EISHIN) の「Beziex Ts」向け開発PCのOSは、本バージョンから Windows 7 に変更している。 |
2010/01/11
| | v0.8.9c |
「制御0」タブを追加し、また「面モード」時に境界をクリックして、その境界の情報を表示する機能を追加。
さらに「制御線」タブを「制御1」タブに変更。そして「全般」タブの「境界曲線を表示」を全体モード時のみとし、「制御1」タブの「隣接面モード」と「周回面モード」内に「境界曲線」の項目を追加した。 |
2010/05/04
| | v0.8.9d |
「面モード(境界曲線単位)」に「等パラメータ線(1/3値)」を追加。また開発環境を Visual C# 2010 に更新した。 |
2010/12/26
| | v0.8.9e |
「面モード(境界曲線単位)」に「対面(3角曲面で有効)」「3角曲面の情報」を追加。 |
2011/01/01
| | v0.9.0 |
DirectX のライブラリを SlimDX に変更。 |
2011/02/05
| | v0.9.0a |
「全般」タブに「投影方法」を追加。
また "net40\x86" の SlimDX.dll を使用することにした。そこで対象フレームワークを「.NET Framework 4.0」に変更(今までは「.NET Framework 3.5」)。 |
2011/02/19
| | v0.9.0b |
「制御0」タブ→「等パラメータ線(1/3値)」→「3角曲面の情報」をチェックボックスに変更し、「縦(1/2値)」を追加(「両方」ラジオボタンは削除)。
また「回転等」タブ→「回転」に、「Z軸回転」スライダを追加した。 |
2011/03/09
| | v0.9.0c |
「制御0」タブ→「等パラメータ線(1/3値)」→「3角曲面の情報」に「縦(1/2値) の交点」を追加。 |
2011/03/14
| | v0.9.1 |
「3角曲面」生成の際に補正アルゴリズムを追加した。これにより例えば、"球の一部を成す3角曲面(実際には近似)" を、より球面に近づけることが可能になった。またパラメータ値のブレもわずかになったので、「等パラメータ線(1/3値)」の "最終形" の曲線が、"初期値"、"中間形" に近くなっているのが分かると思う。
なおこの補正アルゴリズムは「縦(1/2値) の交点」の情報を利用している。 |
2011/03/19
| | v0.9.1a |
「全般」タブのオブジェクトに「OvalEarth4x4」を追加。 |
2011/03/26
| | v0.9.1b |
「全般」タブのオブジェクトに、いくつか形状を追加。また「制御0」タブ→「等パラメータ線(1/3値)」の「中間形(法線補正)」を「中間形(前-内部生成)」に改称した。 |
2011/05/03
| | v0.9.2 |
"内部制御点の元となる「基準内部制御点」" の定義方法を 1種類→2種類に増やした。また「制御0」タブの「境界を横断する制御線」に「中間形(前-内部生成)」を追加し、「等パラメータ線(1/3値)」に「中間形(前-内部生成)の制御線」を加えた。さらに「全般」タブのオブジェクトに形状を追加。
そしてまた使用する SlimDX SDK のバージョンを "(March 2011)" に更新した。 |
2011/05/14
| | v0.9.2a |
「全般」タブのオブジェクトに「SixRadial」を追加。 |
2011/06/03
| | v0.9.3 |
「延長境界曲線」に対応した。また「全般」タブのオブジェクトに「ExtendEdge0」を追加し、「SixRadial」を「SixRadial0」に変更。 |
2011/06/11
| | v0.9.3a |
「直接情報」の境界曲線に対応するとともに、「全般」タブに「境界曲線の別色化」を追加。また「全般」タブのオブジェクトに「EdgeDirect」を加えた。 |
2011/06/13
| | v0.9.3b |
「全般」タブのオブジェクトに「SixRadial1」を追加。 |
2011/07/02
| | v0.9.4 |
例えば「"延長境界曲線" を挟んで、左側に2個の面、右側に1個の面」とすることが出来るようにした。また「全般」タブのオブジェクトに「SixRadial2」を追加。 |
2011/07/24
| | v0.9.5 |
「オーバーレイ」機能を追加した。それに伴い「全般」タブ内「境界曲線の別色化」に「オーバーレイ境界」ラジオボタン等を加えた。また「全般」タブのオブジェクトに「SixRadial3」を追加。 |
2011/10/10
| | v0.9.6 |
当バージョンは「v0.9.5」と機能的にはほぼ同じだが、コードは大幅に変更されている。コード変更の理由は、「v0.9.5」の延長では もはや拡張が困難になってきたからだ。
なお「オーバーレイ」部分は「全体モード」を除き未完成なので、他のモードでは正しくない表示となる場合がある。
また SlimDX SDK を "(March 2011)" から "(September 2011)" に変更した。 |
2011/10/17
| | v0.9.6a |
「オーバーレイ」部分に関して、(「全体モード」に加え) 「周回面モード」での表示も正常になるようにした。なお「面モード」や「隣接面モード」については、まだ未完成である。 |
2011/10/20
| | v0.9.6b |
「オーバーレイ」部分に関して、「隣接面モード」("オーバーレイ中央境界曲線" のクリックを除く)での表示も正常になるようにした(まだ「面モード」については未完成)。 |
2011/10/22
| | v0.9.6c |
「隣接面モード」で "オーバーレイ中央境界曲線" のクリックにも対応した(残りは「面モード」のみ未完成)。 |
2011/11/03
| | v0.9.6d |
「オーバーレイ」部分に関して「面モード」にも対応 (これですべてのモードに対応したことになる)。
さらに「面モード(全体)」に「オーバーレイ」項目を追加し、またこの「面モード(全体)」を「制御1」タブに移した。 |
2011/12/04
| | v0.9.7 |
境界横断導関数の曲率 0 にして接続させるための実験データ「SixRadial4」「FourRadial8」を追加。 |
2012/01/22
2012/02/12
| | v0.9.7b |
「全般」タブのオブジェクトに「Wavy」を追加。 |
2012/05/06
| | v0.9.7c |
「全般」タブのオブジェクトに「Pudding」を追加。 |
2012/05/10
| | v0.9.7d |
「全般」タブのオブジェクトに「SwelledCube」を追加。 |
2012/05/13
| | v0.9.7e |
「全般」タブのオブジェクトに「SphericalCube2」を追加し、「SphericalCube」を「SphericalCube1」に変更。 |
2012/05/28
| | v0.9.8 |
「制御0」「制御1」タブの「境界を横断する制御線」にある、「t成分」の名称を「ベースCBD」に変更。また「SlimDX SDK」を(January 2012)に更新した。さらにZIPファイルに含まれる BeziexTs-TechGuide.pdf も更新。 |
2012/06/10
| | v0.9.8a |
ZIPファイルに含まれる BeziexTs-TechGuide.pdf を更新。 |
2012/06/30
2012/07/05
| | v0.9.8c |
ZIPファイルに含まれる BeziexTs-TechGuide.pdf を更新。 |
2012/07/13
2012/07/16
| | v0.9.8e |
ZIPファイルに含まれる BeziexTs-TechGuide.pdf を更新。 |
2012/09/26
| | v0.9.9 |
「Beziex PCC」機能を追加(「全般」タブのオブジェクトに「CCSubdivSphere」「CCSubdivCup」を加えた)。また「全般」タブに「ベースポリゴンを表示(CCSubdivデータの場合)」を追加。
さらにZIPファイルに含まれる BeziexTs-TechGuide.pdf も更新。 |
2012/09/28
| | v1.0.0 |
ライセンスを、「GPL」と「二条項BSDライセンス」のデュアルライセンスに変更。ちなみに v1.0.0 未満のバージョンは「二条項BSDライセンス」のみである。 |
2012/09/29
| | v1.0.1 |
「Beziex PCC」の一部アルゴリズム変更。 |
2012/10/06
| | v1.0.1a |
ZIPファイルに含まれる BeziexTs-TechGuide.pdf を更新。 |
2012/10/22
| | v1.1.0 |
ZIPファイルに含まれる BeziexTs-TechGuide.pdf を更新。この BeziexTs-TechGuide.pdf は、とりあえず完成。 |
2016/05/07
| | v1.1.0a |
Windows10で、「テキスト、アプリ、その他の項目のサイズを変更する」が100%以外の場合にも対応。 |
9-2. 履歴(Beziex Ts テクニカルガイド)
| | また "2-5. 境界曲線の制限事項(「ベース境界曲線投影平面」関連)" を修正。 |
| |
4. 「4角Beziex曲面」
5. 「3角Beziex曲面」
|
| | また "6-1-6. 「延長境界曲線」の別パターン" を追記。 |
| 2012/09/26 | "3-9. ベクトル q の3次元化" に加筆。 |
| |
7. パッチ型Catmull-Clarkサブディビジョン
|
10. 使用許諾条件
本ソフトウェア(Beziex Ts)は、「GPL」と「二条項BSDライセンス (2-clause BSD license)」のデュアルライセンスであり、本ソフトウェアの利用者はこのソフトウェアを利用または再配布するためにいずれかのライセンスを選ぶことができる。
なお各ライセンスの詳細は、下記のサイトを参照のこと。
ただし上記ライセンスに関わらず、本ソフトウェアはあくまでも研究用なので、商用/非商用を問わず他のソフトウエアに組み込むことは推奨しない。
またデュアルライセンスとなったのは Beziex Ts v1.0.0 以降であり、それ未満のバージョンでは「二条項BSDライセンス」のみとなっている。
11. ダウンロード
[参考] ダウンロードファイルは "ZIP形式" でアーカイブされている。これをNTFSフォーマットのディスクにダウンロードした場合は、まず最初にZIPファイルを右クリックして「プロパティ」メニューを選択し、「プロパティ」ダイアログを表示させる。そしてダイアログの「全般」タブ内の「ブロックの解除」ボタンをクリックすると良い(その後、「OK」もしくは「適用」ボタンをクリックすること)。
これにより "ZIP解凍時" や "一番最初にslnファイルを開く時" に余計なメッセージが出なくなるので、わずらわしさが減ることになる。
なおFAT32フォーマットのディスクにダウンロードした場合は、この操作は不要である。
(C)1999-2016 EISHIN, All Rights Reserved.

|